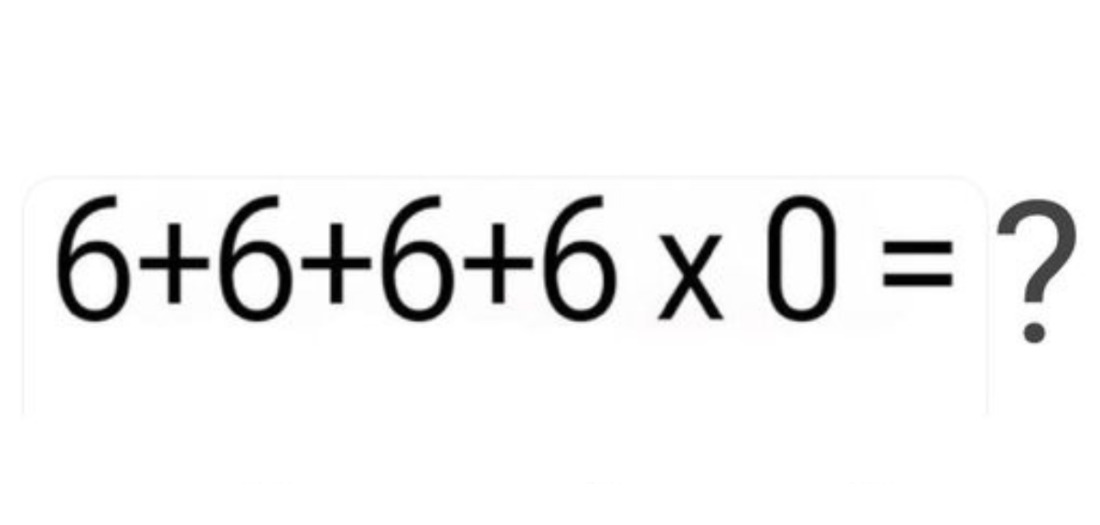Op sociale media wordt momenteel een levendig debat gevoerd over een bijzonder rekensommetje: wat is de uitkomst van 6 + 6 + 6 + 6 x 0? Deze vraag heeft geleid tot een duidelijke verdeeldheid onder de deelnemers, waarbij sommige mensen het antwoord 0 geven, terwijl anderen beweren dat het 24 is. Dit fenomeen roept interessante vragen op over ons begrip van wiskunde en de vaardigheden die nodig zijn voor probleemoplossing. Het feit dat een ogenschijnlijk eenvoudige berekening zoveel verwarring kan veroorzaken, suggereert dat ons begrip van basis wiskundige principes misschien niet zo solide is als we vaak denken. Deze discussie benadrukt niet alleen het belang van nauwkeurig lezen en interpreteren van wiskundige vraagstukken, maar ook de cruciale rol van kritisch denken en logisch redeneren bij het aanpakken van complexere rekensommen.
Content:
Volgorde
Een grondige kennis van basis wiskundige principes, waaronder de volgorde van bewerkingen, is essentieel om deze puzzel correct op te lossen. Dit draagt bij aan betrouwbare en nauwkeurige antwoorden en bevordert een dieper inzicht in wiskundige problemen.

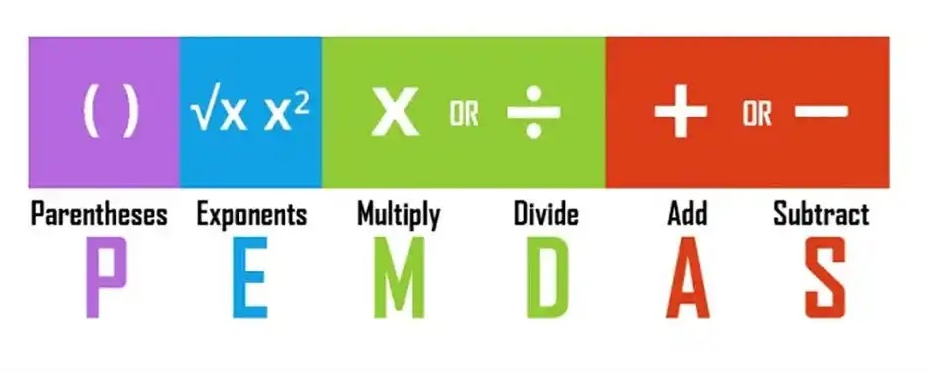
PEMDAS is een acroniem dat staat voor de volgorde van bewerkingen: Parentheses (haakjes), Exponents (machtsverheffingen), Multiplication (vermenigvuldigen) en Division (delen), Addition (optellen) en Subtraction (aftrekken). Dit is een waardevol hulpmiddel dat helpt bij het bepalen van de juiste prioriteiten en het volgen van de correcte volgorde bij het uitvoeren van complexe wiskundige berekeningen, wat leidt tot grotere precisie en efficiëntie.
Parentheses, ook wel haakjes genoemd, kunnen worden gebruikt om extra informatie in een zin te benadrukken of toe te voegen, zodat de lezer de context beter begrijpt en belangrijke details op de juiste waarde kan schatten.
Machtsverheffingen zijn symbolen die in de wiskunde aangeven hoe vaak een bepaald getal met zichzelf moet worden vermenigvuldigd. Ze zijn cruciaal in de algebra en bij functies, omdat ze helpen bij het begrijpen en manipuleren van numerieke uitdrukkingen.
Vermenigvuldigen is een fundamenteel concept in de wiskunde dat van groot belang is voor het samenvoegen van groepen en het berekenen van totale hoeveelheden. Dit is vooral belangrijk bij complexe problemen waarbij verschillende factoren moeten worden samengevoegd voor een nauwkeurig antwoord.
Delen is een wiskundige handeling waarbij een hoeveelheid in gelijke delen wordt verdeeld. Dit wordt vaak gebruikt bij het verdelen van objecten in gelijke delen en bij het uitvoeren van ingewikkelde berekeningen die eenvoudige delingen vereisen.
Optellen, een essentieel aspect van de wiskunde, houdt in dat cijfers worden gecombineerd om een totaal te berekenen. Dit proces wordt regelmatig toegepast in tal van alledaagse situaties, van boodschappen doen tot het beheren van financiën.
Aftrekken, ook wel bekend als minnen, is de wiskundige handeling waarbij je één getal van een ander afhaalt om het verschil tussen deze twee waarden te bepalen. Deze techniek komt vaak voor in verschillende wiskundige berekeningen en is cruciaal bij het oplossen van wiskundige problemen.
In onze puzzel is er een strikte hiërarchie waarin vermenigvuldigen en delen voorrang hebben boven optellen en aftrekken. Het is daarom van groot belang om deze volgorde goed toe te passen om tot de juiste oplossing te komen.
Uitleg
Het is cruciaal om de vergelijking op te lossen volgens de regels van PEMDAS om de exacte uitkomst te vinden: begin met Parentheses, gevolgd door Exponenten, dan Vermenigvuldigen en Delen (van links naar rechts), en tot slot Optellen en Aftrekken (ook van links naar rechts).
- Begin met het vermenigvuldigen van 6 met 0, wat resulteert in 0, voordat je de rest van de berekening uitvoert. Dit is een belangrijke eerste stap die de rest van het probleem beïnvloedt.
- Om de vergelijking correct op te lossen en het juiste resultaat te vinden, moet je de gelijkheid herschrijven met de juiste waarden, namelijk 6 plus 6 plus 6 plus 0.
- Start met het optellen van 6 + 6, wat 12 oplevert. Ga vervolgens verder met 12 + 6, wat gelijk is aan 18. Voeg daarna 0 toe aan 18 en je komt uit op 18 + 0 = 18. Dit laat zien dat de som van drie zessen samen 18 oplevert, wat aantoont dat herhaald optellen van 6 resulteert in een totaal van 18.
De correcte uitkomst van de puzzel is 18, wat betekent dat de som van de betrokken cijfers gelijk is aan dit getal. Onze berekeningen blijken juist te zijn, wat ons vertrouwen in de nauwkeurigheid van de oplossing versterkt.
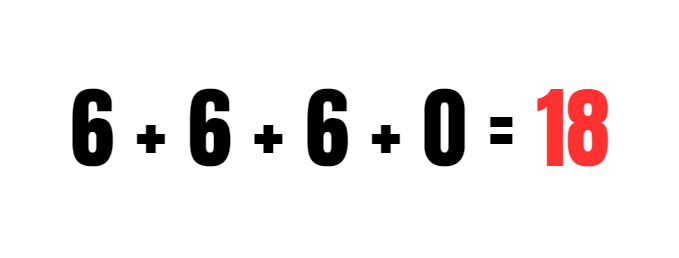
Fouten
Bij het oplossen van wiskundige vergelijkingen, zoals in dit puzzelvoorbeeld, wordt vaak de volgorde van bewerkingen over het hoofd gezien. Dit kan ertoe leiden dat belangrijke stappen worden overgeslagen en dat onnauwkeurige antwoorden worden verkregen.

Veel mensen maken de vergissing te denken dat getallen in de volgorde waarin ze verschijnen moeten worden opgelost, wat leidt tot onjuiste antwoorden zoals 0. Het is cruciaal om eerst de juiste wiskundige bewerkingen uit te voeren voordat we het eindresultaat bepalen.

In informele situaties, waar snelheid van groot belang is, kan de eenvoud van een rekensom misleidend zijn. Dit leidt vaak tot het negeren van de noodzaak voor correcte wiskundige principes, vooral wanneer er een tijdsdruk is.
Wiskunde
Deze uitdaging illustreert de cruciale rol van wiskundige principes bij het oplossen van complexe problemen in diverse situaties. Een diepgaand begrip en de nauwkeurige toepassing van wiskundige concepten en methoden zijn essentieel voor het ontwikkelen van effectieve oplossingen.

Het is van vitaal belang om de juiste volgorde van bewerkingen te begrijpen en toe te passen in verschillende contexten, zoals het berekenen van fooien, het opstellen van budgetten, en het oplossen van wiskundige vraagstukken die op sociale media worden gepresenteerd.

Het is uiterst belangrijk om regelmatig de oplossingen van vergelijkingen te herzien en te controleren om eventuele fouten te voorkomen. Dit helpt de nauwkeurigheid en betrouwbaarheid van de berekeningen te waarborgen.

Kernpunten
- De wiskundige puzzel luidt: vier keer zes optellen en vervolgens het resultaat vermenigvuldigen met nul leidt tot een totaal van achttien, wat aantoont dat zelfs eenvoudige berekeningen complexe uitkomsten kunnen voortbrengen.
- Het begrijpen en correct toepassen van het acroniem PEMDAS is van cruciaal belang voor het oplossen van wiskundige problemen. Door de bewerkingen in deze specifieke volgorde zorgvuldig te volgen, kunnen we fouten minimaliseren en een nauwkeurige oplossing bereiken.
- Het onder de aandacht brengen van fouten die kunnen optreden wanneer de volgorde van bewerkingen niet gerespecteerd wordt, benadrukt de noodzaak van een degelijke wiskundige basis en het zorgvuldig volgen van stappen bij het oplossen van problemen, zoals het negeren van wiskunderegels.
- Wiskundige principes zijn van groot nut in ons dagelijks leven, zoals bij het nauwkeurig afmeten van ingrediënten, het efficiënt plannen van routes en het effectief beheren van financiën en budgetten.
- Het is belangrijk om regelmatig te reflecteren op onze aanpak, omdat dit kan helpen om fouten te voorkomen, de efficiëntie te verhogen, de kwaliteit van besluitvorming te verbeteren en de kans op succes bij het aanpakken van uitdagingen te vergroten.
DEEL NU: Dit soort vergissingen komen vaak voor bij iedereen! 🤓
Dit artikel is met aandacht vervaardigd door LeesPauze, een levendig mediaplatform gewijd aan het verspreiden van zowel inspirerende als informatieve verhalen uit elke uithoek van de wereld. Zorg ervoor dat je op de hoogte blijft van onze meeslepende content door LeesPauze te volgen op Facebook.