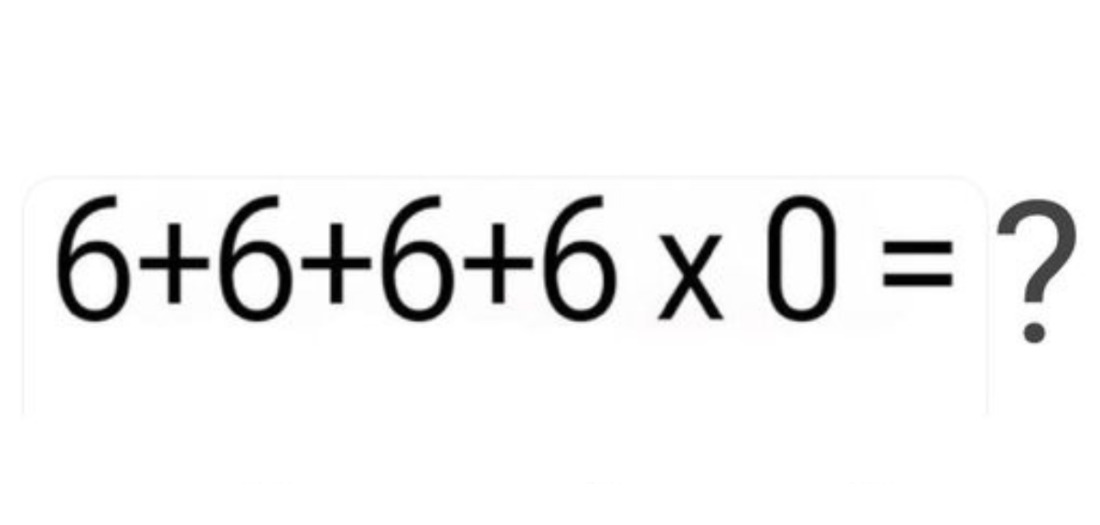In de huidige digitale wereld van sociale media woedt er een levendig debat over een intrigerende wiskundepuzzel: 6 + 6 + 6 + 6 x 0. De meningen zijn sterk verdeeld, met sommige mensen die vasthouden aan het antwoord 0, terwijl anderen 24 als correct beschouwen. Dit controversiële onderwerp roept belangrijke vragen op over ons begrip van wiskunde en probleemoplossing. Vele mensen zijn hierdoor gestimuleerd om na te denken over de juiste aanpak bij het oplossen van dit soort wiskundige vraagstukken, en hoe deze denkprocessen ons intellectuele vermogen kunnen beïnvloeden. Bovendien is er een bredere reflectie op de impact die dit heeft op onze algehele cognitieve ontwikkeling.
Content:
Volgorde
Een grondige kennis van de fundamentele principes van de wiskunde, waaronder de volgorde van bewerkingen, is essentieel voor het nauwkeurig oplossen van de puzzel. Dit zorgt niet alleen voor consistente en correcte wiskundige resultaten, maar biedt ook een dieper inzicht in de aard van de probleemstellingen waarmee we worden geconfronteerd.

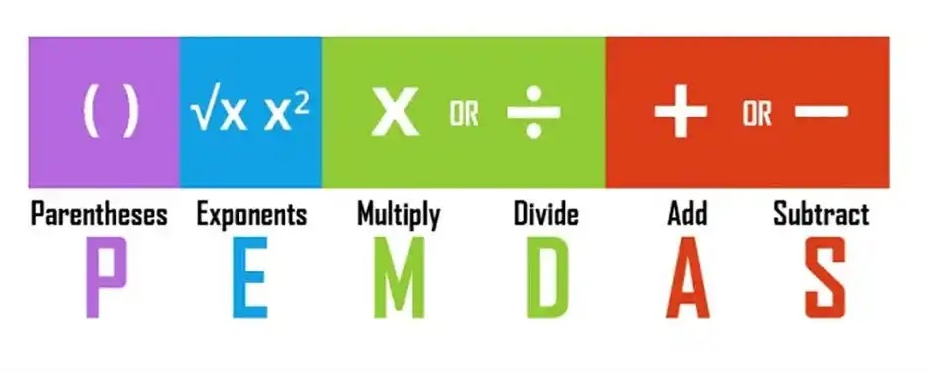
De afkorting PEMDAS is cruciaal voor het correct en efficiënt prioriteren en uitvoeren van complexe wiskundige berekeningen. Deze afkorting staat voor Parentheses (haakjes), Exponents (exponenten), Multiplication and Division (vermenigvuldigen en delen), Addition and Subtraction (optellen en aftrekken).
Haakjes, ofwel parentheses, zijn een krachtig hulpmiddel in de wiskunde. Ze worden gebruikt om aanvullende informatie te accentueren of om specifieke delen van een uitdrukking te markeren, waardoor het voor lezers eenvoudiger wordt om de context te begrijpen en belangrijke details te interpreteren.
Machtsverheffingen spelen een belangrijke rol in de wiskunde: ze verhogen een getal tot een bepaalde macht. Dit concept is van cruciaal belang voor herhaalde vermenigvuldiging en is fundamenteel voor het begrijpen van algebra, functies en het manipuleren van numerieke uitdrukkingen.
Het beheersen van de vermenigvuldiging is van groot belang, omdat het zowel het samenvoegen van gelijke groepen als het herhaaldelijk optellen van getallen omvat om de totale hoeveelheid te berekenen. Deze vaardigheid is onmisbaar voor het oplossen van meer complexe wiskundige vraagstukken.
“Delen is het proces waarbij getallen worden verdeeld, en het helpt om te bepalen hoe vaak een bepaald getal kan worden afgetrokken. Deze handeling is fundamenteel voor het eerlijk verdelen van items in gelijke porties en maakt het mogelijk om ingewikkelde berekeningen uit te voeren door gebruik te maken van eenvoudige delingen.”
Het optellen van losse getallen om de totale som te berekenen, is een fundamentele wiskundige handeling die cruciaal is in dagelijkse situaties, zoals winkelen, het betalen van rekeningen en het berekenen van tijd.
Aftrekken, ook wel de minusoperatie genoemd, is een belangrijke wiskundige handeling waarbij een getal van een ander getal wordt afgetrokken om het verschil te berekenen. Het beheersen van deze bewerking is essentieel in de wiskunde, omdat het helpt bij het oplossen van diverse vraagstukken en het begrip van getallen vergroot.
Bij het oplossen van de puzzel is het cruciaal om te onthouden dat vermenigvuldiging en deling prioriteit hebben boven optellen en aftrekken. Dit betekent dat deze specifieke bewerkingen als eerste moeten worden uitgevoerd om het juiste antwoord te verkrijgen.
Uitleg
Het is van groot belang om de vergelijking correct op te lossen door de richtlijnen van PEMDAS te volgen, wat staat voor Parentheses, Exponenten, Vermenigvuldigen, Delen, Optellen en Aftrekken, om zo de exacte oplossing te vinden.
- Start met het vermenigvuldigen van 6 met 0, wat resulteert in 0. Dit vormt de basis waarop je de overige stappen kunt uitvoeren om de totale som te berekenen en uiteindelijk tot een definitieve uitkomst te komen.
- Om de vergelijking op de juiste manier op te lossen en het juiste eindresultaat te krijgen, moet je het resultaat in de vergelijking vervangen door het correcte antwoord van de som van 6 plus 6 plus 6 plus 0, zodat je de juiste uitkomst kunt bepalen.
- Begin met het berekenen van de som van 6 + 6, wat gelijk is aan 12. Voeg vervolgens 6 toe aan 12 om tot 18 te komen, en voeg ten slotte 0 toe om het eindresultaat van 18 te behalen. Op deze manier wordt aangetoond dat de som van 6, 6 en 6 gelijk is aan 18.
Het correcte antwoord op onze puzzel is dus 18. Dit betekent dat de totale som van de gezochte getallen gelijk is aan dit getal, wat bevestigt dat onze berekeningen juist zijn. Dit vergroot ons vertrouwen in de nauwkeurigheid van onze puzzeloplossing aanzienlijk.
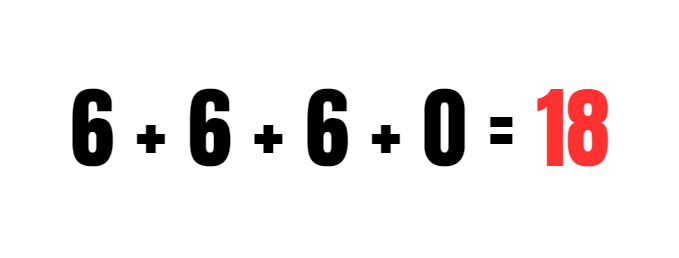
Fouten
Bij het oplossen van wiskundige vergelijkingen, zoals in deze puzzel, worden belangrijke stappen vaak over het hoofd gezien doordat de volgorde van bewerkingen niet correct wordt nageleefd. Dit kan leiden tot onjuiste antwoorden, wat de noodzaak onderstreept om aandacht te besteden aan elk detail.

Er is vaak de misvatting dat getallen in de volgorde waarin ze voorkomen opgelost moeten worden, wat kan resulteren in foutieve antwoorden zoals 0. Het is daarom van essentieel belang om eerst de juiste wiskundige bewerkingen uit te voeren voordat je het uiteindelijke antwoord berekent.

In situaties waar de snelheid van groot belang is en beslissingen snel genomen moeten worden, worden de juiste wiskundige principes vaak over het hoofd gezien. Dit gebeurt doordat de eenvoud van de vergelijkingen misleidend kan zijn, wat kan leiden tot onjuiste conclusies.
Wiskunde
Deze situatie benadrukt het belang van wiskundige principes bij het oplossen van complexe problemen in uiteenlopende situaties. Een diepgaand begrip van wiskundige concepten en methoden is noodzakelijk om effectieve en doeltreffende oplossingen te kunnen ontwikkelen.

Het is van groot belang om de juiste volgorde van bewerkingen te begrijpen en deze correct toe te passen in verschillende contexten, zoals het berekenen van tips, het opstellen van een budget of het oplossen van een wiskundig probleem dat op sociale media wordt gepresenteerd.

Het is uiterst belangrijk om regelmatig te controleren of de oplossingen van de vergelijkingen juist zijn om fouten te voorkomen en de nauwkeurigheid van de berekeningen te waarborgen.

Kernpunten
- De wiskundige puzzel die moet worden opgelost luidt als volgt: Als je het getal zes vier keer bij elkaar optelt en daarna vermenigvuldigt met nul, is het totale resultaat achttien. Dit voorbeeld illustreert dat zelfs ogenschijnlijk eenvoudige berekeningen tot verwarrende en onverwachte uitkomsten kunnen leiden.
- Om wiskundige problemen correct en effectief op te lossen, is het van cruciaal belang om het acroniem PEMDAS te begrijpen en op de juiste manier toe te passen. Dit acroniem verschaft ons de juiste volgorde van bewerkingen en voorkomt dat we fouten maken door onnauwkeurigheid.
- Een solide wiskundige basis en het volgen van de juiste stappen zijn van grote waarde bij het oplossen van problemen, vooral wanneer fouten ontstaan door het niet naleven van de bewerkingsvolgorde en het niet respecteren van de fundamentele regels van de wiskunde.
- Wiskundige principes zijn van onschatbare waarde in verschillende facetten van ons dagelijkse leven, zoals het nauwkeurig afmeten van ingrediënten tijdens het koken, het effectief plannen van reisroutes, en het efficiënt beheren van onze financiën en budgetten.
- Door regelmatig te reflecteren op onze aanpak kunnen we fouten vermijden, onze efficiëntie verbeteren, weloverwogen beslissingen nemen en effectief reageren op de uitdagingen waarmee we geconfronteerd worden.
DEEL NU: 🔍 Het echte antwoord vind je in de allereerste reactie hieronder! 👇📖✨
Dit artikel is met aandacht gecreëerd door LEEF., een bruisend mediaplatform, toegewijd aan het brengen van inspirerende en leerzame verhalen uit elke hoek van de wereld. Zorg dat je op de hoogte blijft van onze meeslepende content door LEEF. te volgen op Facebook onder de naam LEEF.