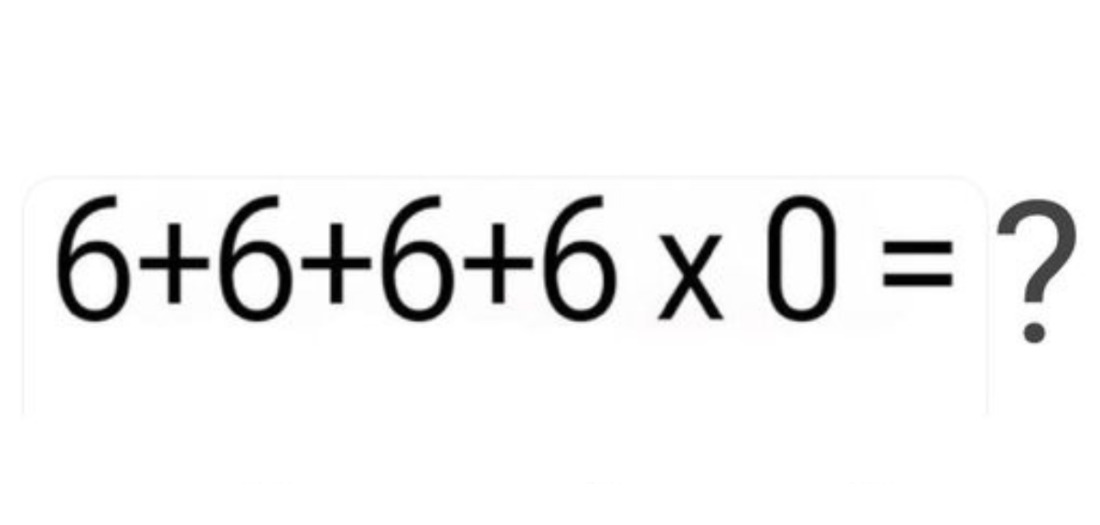In de steeds veranderende digitale wereld van sociale media, waar meningen en discussies continu plaatsvinden, ontstaat er een interessante discussie over de eenvoudige rekensom 6 + 6 + 6 + 6 x 0. Deze puzzel heeft geleid tot verdeeldheid onder mensen, met sommigen die beweren dat het antwoord 0 is en anderen die stellen dat het 24 is. Deze discussie daagt ons uit om na te denken over onze fundamentele kennis van wiskunde en de manier waarop we problemen aanpakken en oplossen.
Content:
Volgorde
Om de puzzel op de juiste manier op te lossen, is het cruciaal om de basisprincipes van wiskunde te begrijpen, vooral de volgorde van bewerkingen. Dit is essentieel voor het verkrijgen van consistente en correcte oplossingen, en draagt bij aan een dieper inzicht in hoe problemen moeten worden aangepakt en opgelost.

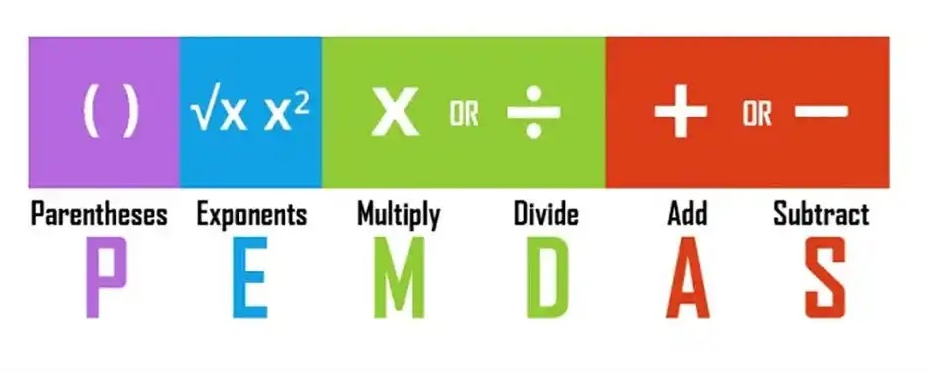
Het acroniem PEMDAS, dat staat voor Parentheses (haakjes), Exponents (exponenten), Multiplication (vermenigvuldiging), Division (deling), Addition (optelling) en Subtraction (aftrekking), helpt ons bij het prioriteren van wiskundige bewerkingen. Dit acroniem is essentieel voor het uitvoeren van berekeningen in de juiste volgorde en speelt een belangrijke rol in het waarborgen van nauwkeurigheid en efficiëntie in wiskundig denken en handelen.
Haakjes, of parentheses, worden gebruikt om extra informatie binnen een zin af te bakenen, zodat de lezer de context of aanvullende details beter kan begrijpen. Dit helpt bij het verduidelijken van de volledige betekenis van een zin.
Machtsverheffen, of exponents, zijn symbolen die de kracht van een basisgetal aangeven en worden gebruikt om herhaalde vermenigvuldiging uit te voeren. Ze spelen een cruciale rol in algebra en andere wiskundige functies.
Vermenigvuldiging is een fundamentele wiskundige bewerking waarbij een getal herhaaldelijk bij zichzelf wordt opgeteld om de totale hoeveelheid te bepalen. Het vormt een basiskennis van wiskunde die nodig is voor het oplossen van complexere problemen en berekeningen.
Delen is een basis rekenkundige bewerking die wordt gebruikt om een hoeveelheid op te splitsen in gelijke delen. Dit helpt bij het vaststellen hoe vaak een getal kan worden afgetrokken van een ander getal. Deze wiskundige handeling is essentieel voor het verdelen van items of numerieke waarden in gelijke proporties en maakt complexe berekeningen en verdelingen mogelijk.
Optellen is de basiswiskunde waarbij twee of meer getallen worden samengevoegd om de totale som te berekenen. Dit proces is essentieel voor dagelijkse activiteiten, van het doen van boodschappen tot het uitvoeren van financiële transacties.
Aftrekken, ook wel bekend als min, is het proces waarbij één getal van een ander wordt afgetrokken om het verschil te vinden. Deze basisbewerking is essentieel in de rekenkunde.
De hiërarchie van wiskundige bewerkingen benadrukt dat vermenigvuldiging en deling voorrang hebben boven optellen en aftrekken. Deze prioriteit is cruciaal voor het vinden van het juiste antwoord in onze puzzel en speelt een belangrijke rol bij het bereiken van de gewenste oplossing.
Uitleg
Het is van groot belang om de rekensom op te lossen volgens de regels van PEMDAS, die staan voor Parentheses (haakjes), Exponents (exponenten), Multiplication (vermenigvuldiging) en Division (deling) (van links naar rechts), en Addition (optelling) en Subtraction (aftrekking) (ook van links naar rechts). Deze volgorde van bewerkingen helpt ons om de exacte oplossing te vinden.
- Begin met de vermenigvuldiging: vermenigvuldig 6 met 0, wat resulteert in 0. Daarna ga je verder met de rest van de berekening.
- Vervang het resultaat van de vermenigvuldiging in de oorspronkelijke vergelijking door 0, en voer vervolgens de optelling uit: 6 + 6 + 6 + 0.
- Voer de optelling stap voor stap uit: 6 + 6 = 12, vervolgens 12 + 6 = 18, en voeg tenslotte 0 toe, wat resulteert in 18 + 0 = 18 als eindresultaat.
Het juiste antwoord op de puzzel is 18. Dit betekent dat de som van de getallen in de puzzel optelt tot dit getal, en onze berekeningen zijn correct uitgevoerd.
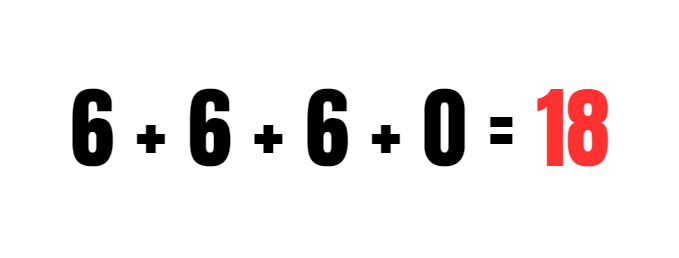
Fouten
Bij het oplossen van wiskundige vergelijkingen, zoals deze puzzel, maken mensen vaak de fout door de bewerkingsvolgorde te negeren. Dit kan leiden tot gemiste stappen en onjuiste antwoorden.

Veel mensen maken ten onrechte de aanname dat de getallen in de volgorde van verschijnen moeten worden opgelost. Dit leidt vaak tot foutieve antwoorden zoals 0, omdat ze niet inzien dat de juiste volgorde van bewerkingen gevolgd moet worden voordat een antwoord kan worden berekend.

De schijnbare eenvoud van de puzzel kan misleidend zijn, waardoor het belang van correcte wiskundige principes vaak over het hoofd wordt gezien. Dit gebeurt vooral wanneer men onder tijdsdruk staat of in informele situaties waarin snelheid voorop staat ten koste van zorgvuldigheid en precisie.
Wiskunde
Deze uitdaging benadrukt het belang van wiskundige principes bij het oplossen van problemen in diverse situaties. Of het nu gaat om het berekenen van een fooi, het opstellen van een budget, of het oplossen van een probleem op sociale media, het correct begrijpen en toepassen van de volgorde van bewerkingen is cruciaal.

Het correct begrijpen en toepassen van de volgorde van bewerkingen is essentieel in verschillende situaties. Dit geldt niet alleen voor wiskundige problemen, maar ook voor dagelijkse taken zoals het berekenen van een fooi, het plannen van een budget, of het oplossen van problemen in alledaagse scenario’s.

Het is van vitaal belang om altijd de tijd te nemen om een berekening zorgvuldig te controleren. Dit helpt om eventuele fouten te voorkomen en zorgt ervoor dat de berekeningen correct zijn en de integriteit van de resultaten gewaarborgd blijft.

Kernpunten
- De wiskundige puzzel die we onderzoeken, luidt: als je vier keer het getal zes bij elkaar optelt en het resultaat vervolgens vermenigvuldigt met nul, wat is dan het uiteindelijke antwoord? Het antwoord is niet 0 of 24, maar 18.
- Het begrijpen en correct toepassen van het acroniem PEMDAS, dat staat voor Parentheses (haakjes), Exponents (exponenten), Multiplication (vermenigvuldiging) en Division (deling) (van links naar rechts), en Addition (optelling) en Subtraction (aftrekking) (ook van links naar rechts), is van groot belang bij het oplossen van wiskundige problemen. Dit acroniem geeft de juiste volgorde aan waarin bewerkingen moeten worden uitgevoerd en helpt bij het voorkomen van fouten die kunnen optreden bij het niet strikt volgen van deze volgorde.
- Fouten die ontstaan door het negeren van de bewerkingsvolgorde, zoals het niet naleven van wiskundige regels, benadrukken het belang van een goede wiskundige opleiding en het zorgvuldig volgen van stappen bij het oplossen van vraagstukken.
- Wiskundige principes zijn van essentieel belang in veel dagelijkse situaties. Of het nu gaat om het berekenen van ingrediënten voor recepten, het plannen van efficiënte routes voor dagelijkse verplaatsingen, of het beheren van financiële zaken zoals budgettering en investeringen, een goede kennis van wiskunde is cruciaal voor succes.
- Het regelmatig even terugkijken en reflecteren is nuttig om fouten te voorkomen en efficiënter te werken. Reflectie helpt bij het ordenen van gedachten, bedenken van alternatieve oplossingen en overwegen van gevolgen, wat leidt tot beter geïnformeerde beslissingen en effectievere reacties op uitdagingen.
deel nu: Iedereen maakt deze fout regelmatig! 🤓 Het ECHTE antwoord vind je in de eerste reactie hieronder! 📖👀👇
Dit stuk is vakkundig ontwikkeld door KijkTip, een bruisend mediaplatform dat uitblinkt in het presenteren van verhalen die zowel verlichtend als verrijkend zijn, uit de meest diverse delen van de wereld. Zorg dat je altijd verbonden blijft met onze meeslepende updates door KijkTip te volgen op Facebook. Ga met ons mee op een avontuurlijke reis door een wereld van verhalen die impact maken. 🌍✨