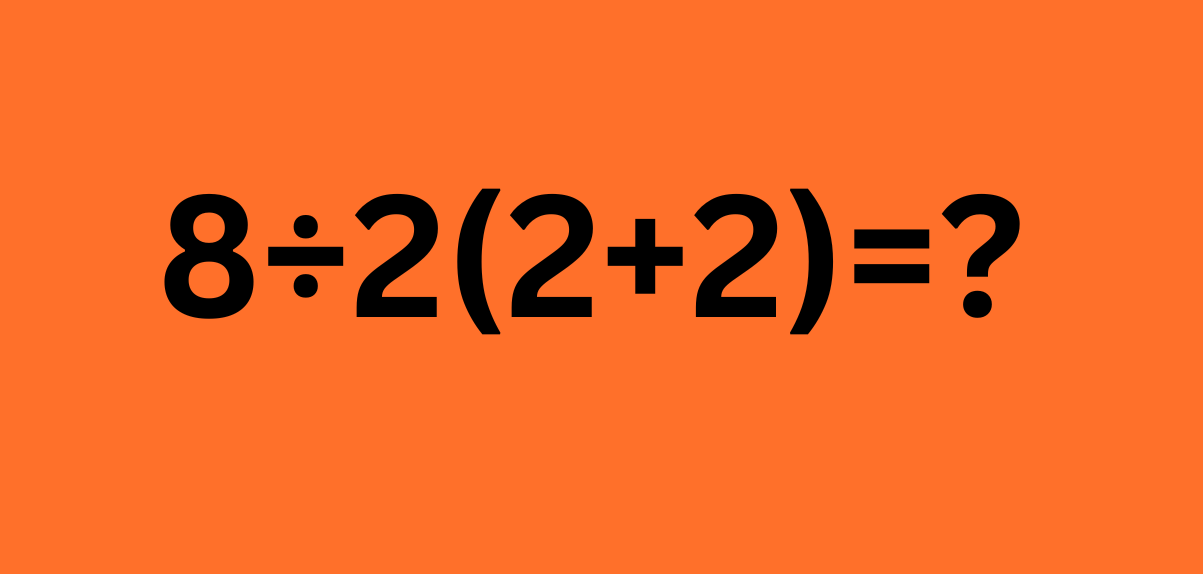Er zijn talloze uitdagende virale puzzels te vinden op het internet die de nieuwsgierigheid van miljoenen mensen prikkelen en hen uitdagen om hun intellectuele capaciteiten te verbeteren. In 2019 zorgde één wiskundig probleem wereldwijd voor verhitte discussies en verbazing, wat de vraag opriep hoe zo’n ogenschijnlijk simpele som zoveel opschudding kon veroorzaken en zo’n impact kon hebben op de online gemeenschap.
Dit raadsel werd gedeeld in een enkele tweet: 8 ÷ 2(2 + 2). Op het eerste gezicht lijkt het een eenvoudig wiskundeprobleem dat velen van ons waarschijnlijk moeiteloos zouden kunnen oplossen tijdens onze schooljaren.

Mensen ontdekten al snel dat er niet slechts één correct antwoord was, maar dat er daadwerkelijk twee verschillende antwoorden mogelijk waren.

Dit veroorzaakte een diepe verdeeldheid onder de respondenten, waarbij sommigen bleven volharden in de overtuiging dat het juiste antwoord 16 was, terwijl anderen stellig beweerden dat de correcte uitkomst slechts 1 kon zijn.

De online discussie leidde tot verdeelde meningen onder wiskundigen over welke methode correct was, waarbij sommigen beweerden dat de ene benadering beter was, terwijl anderen krachtig vasthielden aan hun overtuiging dat hun methode juist was.

Content:
De Verwarring
Het probleem begon op Twitter toen een gebruiker de som deelde en zijn volgers vroeg om de oplossing te vinden, wat leidde tot uitgebreide discussies over de juistheid van de berekening en verschillende mogelijke strategieën die gebruikt konden worden om het op te lossen.

Al snel stroomde het internet over met een overvloed aan reacties van mensen die verschillende antwoorden gaven en elkaar probeerden te overtuigen met uitgebreide argumenten, talloze bronnenlinks en emotionele betogen die de discussie nog verder aanwakkerden.

Hoe kon een eenvoudige vergelijking zoveel discussie veroorzaken in een tijd waarin communicatie zo snel polarisatie en misverstanden kan veroorzaken en de kloof tussen mensen vergroot?

Om het probleem volledig te begrijpen en effectief aan te pakken, is het van essentieel belang om allereerst de fundamentele basisregels van de wiskunde te begrijpen, waaronder in het bijzonder de volgorde van bewerkingen die cruciaal is voor het correct oplossen van complexe wiskundige vraagstukken.

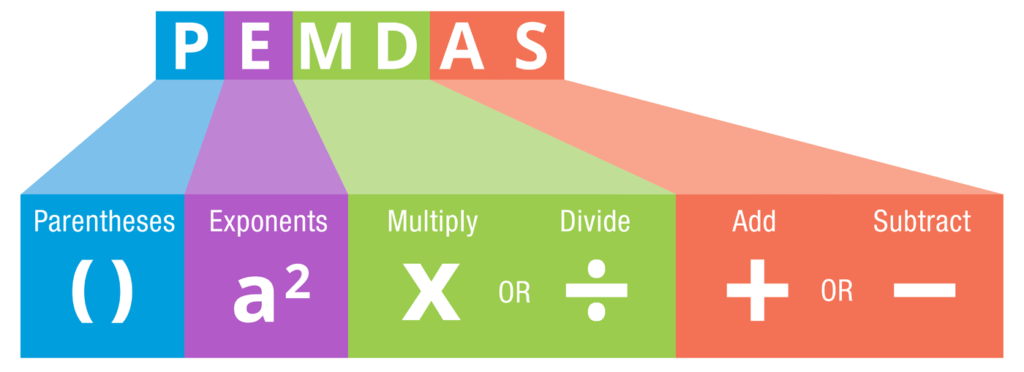
PEMDAS, de sleutel tot het correct oplossen van wiskundige vergelijkingen, staat voor de volgorde waarin bewerkingen moeten worden uitgevoerd: Parentheses (haakjes), Exponents (machten), Multiplication (vermenigvuldiging), Division (delen), Addition (optellen) en Subtraction (aftrekken).
- “Haakjes zijn handige tekens die worden gebruikt om informatie in een zin te verduidelijken of om een extra toelichting te geven op een bepaald onderwerp, waardoor de lezer een beter begrip krijgt van de tekst.”
- E: Exponenten geven aan hoe vaak een getal met zichzelf wordt vermenigvuldigd, wat essentieel is in wiskundige berekeningen om groeisnelheid en -patronen te bepalen.
- Een afkorting voor MD is Vermenigvuldiging en Deling. Deze twee fundamentele wiskundige operaties worden gebruikt om getallen met elkaar te vermenigvuldigen of te delen. Door het toepassen van deze operaties kunnen complexe berekeningen worden uitgevoerd en kunnen verschillende wiskundige problemen worden opgelost.
- “AS: Optellen en aftrekken zijn basisrekenkundige bewerkingen waarbij getallen worden toegevoegd en afgetrokken om een nieuwe uitkomst te krijgen.”
Volgens de regel moeten eerst de bewerkingen binnen haakjes worden opgelost, dan exponenten worden berekend, vervolgens vindt de vermenigvuldiging en deling plaats van links naar rechts, en tot slot worden de optellingen en aftrekkingen uitgevoerd, ook van links naar rechts.
Houd rekening met deze regel bij het oplossen van het wiskundeprobleem: analyseer en pas de formules toe, identificeer en los onbekende variabelen op, en controleer de oplossing op juistheid en consistentie.
- Los de som 8 ÷ 2(4) op door eerst de vermenigvuldiging uit te voeren en vervolgens de deling. Dit betekent dat je 4 vermenigvuldigt met 2 en vervolgens 8 deelt door het resultaat.
- “Delen we eerst 8 door 2, dan vermenigvuldigen we 4 met 4 voor een eindresultaat van 16.”
Volgens deze stappen zou het antwoord op het probleem 16 moeten zijn. Maar bij wiskundige problemen is er vaak een alternatieve methode die tot een ander resultaat leidt, waardoor de oplossing complexer en uitdagender wordt dan gedacht.

Een Alternatieve Interpretatie
De alternatieve aanpak lost het probleem op door de vergelijking anders te interpreteren, waarbij haakjes direct worden vermenigvuldigd met het getal ervoor in plaats van de traditionele links naar rechts aanpak te volgen.
The expression “8 ÷ [2(4)]” is simplified to “8 ÷ [2(4)] = 8 ÷ 8 = 1”, as it involves dividing 8 by the product of 2 and 4, which simplifies to 1.
In deze specifieke situatie wordt de haakjesnotatie beschouwd en behandeld als één ondeelbaar geheel, waardoor de focus eerst ligt op het oplossen van het deel binnen de haakjes. Dit resulteert in een aanpassing van de vergelijking naar:
De berekening van 8 gedeeld door 8 leidt tot een quotiënt van 1, wat betekent dat het delen van 8 door 8 resulteert in een uitkomst van 1.
De oplossing is gebaseerd op interpretatieverschillen over de volgorde van bewerkingen, waarbij sommigen prioriteit geven aan vermenigvuldiging naast haakjes boven deling, wat leidt tot verschillende uitkomsten en mogelijke misverstanden in de berekening.
Hierdoor ontstaan er twee tegengestelde kampen met uiteenlopende standpunten betreffende de vraag, waarbij het ene kamp vol overtuiging beweert dat het juiste antwoord 16 is, terwijl het andere kamp standvastig volhoudt dat 1 het correcte antwoord is.
De Rol Van Conventies
De discussie over dit complexe probleem illustreert hoe zelfs wiskunde, een discipline die vaak wordt gezien als objectief en absoluut, afhankelijk blijkt te zijn van subjectieve conventies en interpretaties die verschillende perspectieven en benaderingen van hetzelfde probleem kunnen openbaren.

In een recent interview zei Mike Breen van de American Mathematical Society dat het antwoord 16 zou moeten zijn volgens de strikte volgorde van bewerkingen, wat aangeeft dat de regels van wiskundige operaties correct zijn toegepast.

Hij merkte echter op dat de vergelijking, zoals geformuleerd, dubbelzinnig is en vatbaar is voor diverse interpretaties, wat het lastig maakt om een heldere conclusie te trekken over de betekenis ervan.

In de wiskunde kunnen soms dubbelzinnigheden ontstaan, ondanks precieze regels van wiskundigen. Meerdere interpretaties zijn mogelijk.
“In dit geval zou ik niet meteen iemand corrigeren die zegt dat het antwoord 1 is, hoewel volgens de conventionele regels 16 het juiste antwoord is,” verklaarde Breen, omdat de vraag verschillende interpretaties toelaat en het belangrijk is om open te staan voor diverse perspectieven.”
De ambiguïteit die inherent is aan wiskunde roept sterke associaties op met andere vormen van taal en cultuur waar conventies een cruciale rol spelen en waar interpretatie een complexe en vaak subjectieve kwestie is, waardoor het begrip en de communicatie van kennis en ideeën soms moeilijk en verwarrend kunnen zijn voor mensen die niet vertrouwd zijn met deze concepten.
Een eenvoudige vergelijking kan verschillende betekenissen hebben afhankelijk van de context, daarom is het essentieel om zorgvuldig na te denken over hoe het wordt toegepast om misverstanden te voorkomen en de boodschap duidelijk over te brengen.
Dit punt werd ook benadrukt door Rhett Allain, een gerespecteerde natuurkundeprofessor aan de Southeastern Louisiana University, tijdens zijn boeiende en informatieve lezing waarin hij dieper inging op de wetenschappelijke principes die ten grondslag liggen aan dit concept.
Hij stelde voor het probleem anders te formuleren zodat de uitkomst zeker 1 zou zijn geweest.
“Allain verklaarde dat conventies cruciaal zijn en benadrukte dat het hanteren van specifieke regels en afspraken voor het opschrijven en interpreteren van informatie net zo essentieel is als onze afspraken over spelling.”
In taal komen variaties voor, zoals het subtiele verschil tussen ‘grijs’ en ‘grijs’ dat misschien alleen zichtbaar is in de context, maar we begrijpen nog steeds moeiteloos de betekenis.
Wat Kunnen We Hieruit Leren?
Het virale wiskundeprobleem toont aan dat zelfs eenvoudige rekensommen voor verwarring en discussie kunnen zorgen als ze niet duidelijk worden gepresenteerd.
Wiskunde heeft strikte regels, maar biedt ruimte voor diverse interpretaties en individuele creativiteit om complexe problemen op te lossen en nieuwe concepten te ontwikkelen.
Dit kan frustratie veroorzaken bij mensen die moeite hebben met wiskundige conventies, maar kan ook leiden tot interessante discussies over hoe ze worden toegepast in ons dagelijks leven.
Duidelijke wiskundige notaties zijn van essentieel belang, aangezien ze, net als taal, soms misleidend kunnen zijn en het daarom cruciaal is voor iedereen om de precieze betekenis achter de symbolen en formules volledig te begrijpen.
Goede communicatie is cruciaal voor succes in professionele en persoonlijke situaties. Het is belangrijk om helder te communiceren en de juiste conventies te volgen om misverstanden te voorkomen en goede relaties op te bouwen.
Key Points:
- Het wiskundeprobleem zorgde voor verdeeldheid online, met verschillende antwoorden variërend van 16 tot 1, wat voor verwarring zorgde over het juiste antwoord.
- Volgens de PEMDAS-regel zou het antwoord op de som 16 moeten zijn, omdat eerst de bewerking binnen de haakjes moet worden uitgevoerd voordat de deling van links naar rechts wordt toegepast.
- Een andere interpretatie van de berekening is dat 8 wordt gedeeld door de uitkomst van 2 keer 4, wat uiteindelijk gelijk is aan 1.
- Wiskundigen, waaronder Mike Breen, waren het oneens over de vraag en verdeelden de vakgemeenschap.
- Het belang van duidelijke en eenduidige wiskundige notaties wordt aangetoond in verschillende situaties, zoals complexe formules, wetenschappelijke onderzoeken en financiële analyses, om verwarring te voorkomen en een correcte interpretatie van de berekeningen te garanderen.
DEEL NU: RAADSEL 🤓Deze wiskundige uitdaging leidt tot intense gesprekken over de juiste oplossing!
Dit artikel is zorgvuldig vervaardigd door Plaatjes Koningin, een levendig mediaplatform dat zich wijdt aan het brengen van inspirerende en verrijkende verhalen uit alle hoeken van de wereld. Om altijd op de hoogte te blijven van onze fascinerende content, volg Plaatjes Koningin op Facebook en duik mee in de wereld van verhalen die ertoe doen. 🌍✨ – Plaatjes Koningin
Dit artikel is informatief, geen professioneel advies. Wij zijn niet verantwoordelijk voor gevolgen van beslissingen op basis van deze informatie. Raadpleeg altijd een professional voor belangrijke beslissingen.